Rubber elasticity
The elasticity of polymer networks was subject to ongoing research in the past 80 years. Starting from the affine and phantom model for non-entangled chains to constrained junction, constrained chain, tube, slip-link or slip tube models for entangled chains, more and more advanced models to describe rubber elasticity have been developed throughout the decades. Despite the large advancements made, the agreement between theory and experimental data is often still unsatisfying.
Computer simulations of model networks are a way to learn about the differences between model assumptions and the structure of networks where the preparation was simulated analogous to the experiments. Quite unexpectedly, the simulation data of several groups showed an increasing suppression of the cross-link fluctuations below the theoretical prediction that one obtains by superposing the confining potentials of entanglements and the phantom modulus [1]. It turned out that the deviations are caused by an increased entanglement contribution that results from linking entangled chains preferably in stretched conformations. Therefore, the elastic modulus is not the simple sum of an unperturbed melt-entanglement contribution and the phantom modulus. This perturbs the classical determination of the cross-link density through modulus and complementary analysis with focus on reaction efficiency becomes desirable.
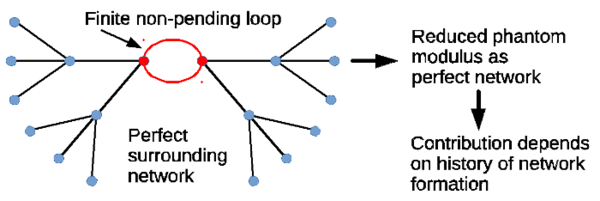
One striking difference between theoretical models for rubber elasticity and the structure of real networks is that one assumes for the former a perfect tree structure without finite loops, while real networks are entirely made of finite loops that consist of order ten or less elastic strands per loop [2]. This challenges the phantom model at its grounds and more advanced models of entangled networks allowing for finite loops need to be elaborated.
A first step towards a solution of this problem is to consider finite non-pending loops in an otherwise perfect surrounding network as shown in the Figure. This problem is exactly solvable, however the solution to this problem did not truly fit to the available simulation data. Similar to the preceding work [1], an excess strain of the network chains was identified, here as a function of the loop size. When correcting for this extra stress, the resulting simulation data was in line with a model, where the loops inside the network optimize independently their conformations like isolated loops, however, these loops are under an average pre-load [2]. Quite interestingly, the formation of finite loops may lead in part to this pre-load, while other contributions stem from driving the reactions to completion. Thus, not only conversion but also the size distribution of finite loops impacts the phantom modulus, which will be elaborated further in future work.
Publications:
- Lang, M.,
Relation between Cross-Link Fluctuations and Elasticity in Entangled Polymer Networks,
Macromolecules 50 (2017) 2547-2555. - Lang, M.,
Elasticity of phantom model networks with cyclic defects,
ACS Macro Letters 7 (2018) 53

