Personal Homepage

Soft-matter systems exhibit nontrivial collective behaviour, e.g. phase transitions and self-assembly. The pervasiveness of soft-matter is impressive with wide ranging applications in industry. However, what makes these systems particularly interesting for physicists is their ubiquity in Biology. For instance, the disordered elastic network shown below is actually found all over in our body. How does this disordered structure impart us mechanical integrity? Surprisingly, even in this system there is a phase transition somewhat analogous to ferromagnetism.
In my group we use the methods of classical statistical mechanics to investigate soft matter, both in and out of equilibrium. This involves the application of computational techniques such as Brownian Dynamics and Monte Carlo simulations and established techniques from liquid-state theory, such as (classical) density functional theory, integral equations, mode-coupling theory etc., as well as the development of new analytic and numerical approaches.
Research Interests
Biopolymer Networks Mechanics
The elastic stress response of living cells and tissues is governed by the viscoelasticity of complex networks of filamentous proteins such as the cytoskeleton and the extracellular matrix. This property of such biological gels not only makes living cells and tissues stiff enough to maintain shape and transmit forces under mechanical stress, but also provides them the compliance to alter their morphology needed for cell motion and internal reorganisation. Unlike ordinary polymer gels and other materials with rubber-like elastic properties however, biological gels behave nonlinearly in response to deformation. One classic feature is strain stiffening, where a moderately increasing deformation leads to a rapid increase in stress within the material.
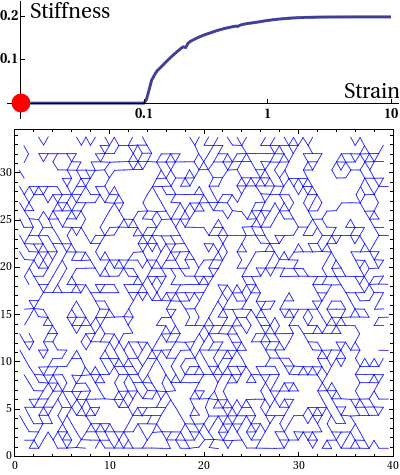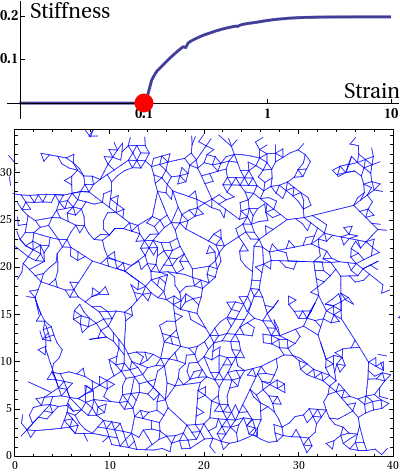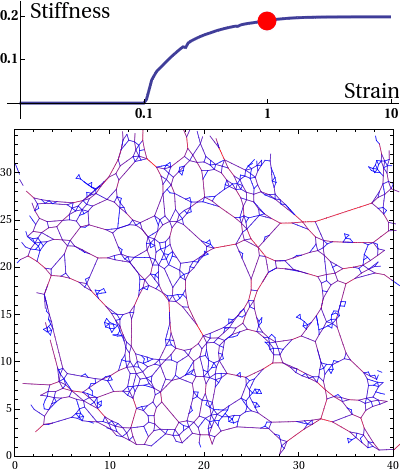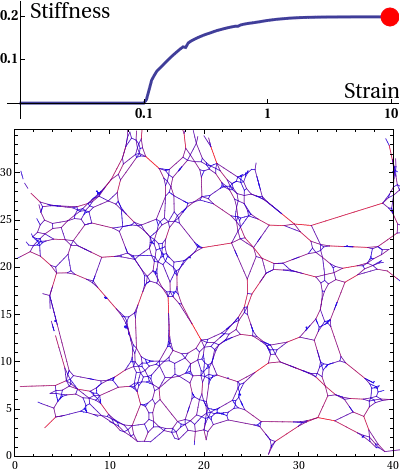
Disordered fiber network subjected to uniform bulk expansion. There is a continuous phase transition from floppy to rigid phase. The nonlinear mechanics of collagen networks can be quantitatively captured by our scaling theory.
Active Matter
Active matter is ubiquitous in Biology. Examples include cytoskeletal molecular motors performing directed motion on filaments inside a cell, nucleic acid motors involved in transcription process inside nucleus, and even microscopic living objects such as the Escherichia coli bacteria which generates motion using helical flagella. The defining characteristic of active matter is that it is intrinsically nonequilibrium. The constituents of active matter generate motion by consuming energy from their local environment. In addition to the solvent-induced Brownian motion, active particles undergo self-propulsion resulting in persistent character of particle trajectories. It is the self-propulsion feature of these particles, generally termed as the activity, which captures the nonequilibrium nature of active matter.
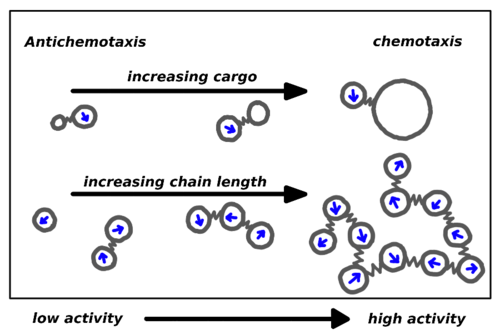
Chemotaxis emerges in a system of cargo-carrying active particles. Whereas the dimer remains in low activity regions for small loads, it moves into the regions of higher activity for heavy loads. The same happens in a system of chains of active particles.
Odd-Diffusive Systems
The characteristic property of an odd-diffusive system is a diffusion tensor which can be decomposed into a symmetric part and an antisymmetric part. Odd-diffusive behaviour emerges naturally in systems with broken time-reversal and parity symmetry. The motion of a charged particle in a magnetic field is a classical example of broken time-reversal symmetry. For this reason, the probability flux associated with a particle performing overdamped motion gets a certain handedness based on the charge it carries. Such a diffusion behaviour is described by a tensor that has anti-symmetric components. Analogous to case of odd-viscosity, recently such diffusive behaviour has aptly been termed as odd-diffusive and has attracted considerable attention.
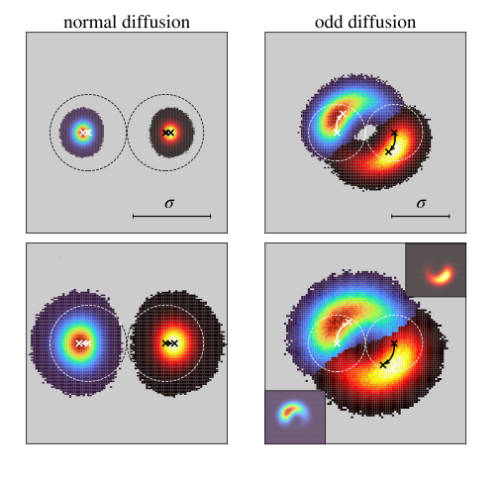
Generally two diffusing particles move away from each other following a collision. Odd-diffusing particles show a strikingly different behaviour: They roll past each other helping each other explore space. An unusual consequence is the enhancement of dynamics due to collisions.
Selected Publications
- Chemotaxis of cargo-carrying self-propelled particles
H. D. Vuijk, H. Merlitz, M. Lang, A. Sharma, J.-U. Sommer, Phys. Rev. Lett. 2021, 126, 208102. - Stochastic resetting of active Brownian particles with Lorentz force
I. Abdoli, A. Sharma, Soft Matter 2021, 17, 1307. - Mean-field theory of inhomogeneous fluids
S. M. Tschopp, H. D. Vuijk, A. Sharma, J. M. Brader, Phys. Rev. E. 2020, 102, 042140. - Scaling theory for mechanical critical behavior in fiber networks
J. Shivers, S. Arzash, A. Sharma, F. C. MacKintosh, Phys. Rev. Lett. 2019, 122, 188003. - Escape rate of active particles in the effective equilibrium approach
A. Sharma, R. Wittmann, J. M. Brader, Phys. Rev. E. 2017, 95, 012115. - Strain-controlled criticality governs the nonlinear mechanics of fibre networks
A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink, F. C. MacKintosh, Nature Physics 2016, 12, 584. - Green-Kubo approach to the average swim speed in active Brownian systems
A. Sharma, J. M. Brader, Journal of Chemical Physics 2016, 145, 161101. - Anomalous Discontinuity at the Percolation Critical Point of Active Gels
M. Sheinman, A. Sharma, J. R. Alvarado, G. H. Koenderink, F. C. MacKintosh, Phys. Rev. Lett. 2015, 114, 098104. - Molecular motors robustly drive active gels to a critically connected state
J. R. Alvarado, M. Sheinman, A. Sharma, F. C. MacKintosh, G. Koenderink, Nature Physics 2013, 9, 591. - Proton migration mechanism for operational instabilities in organic field-effect transistors
A. Sharma, S. G. J. Mathijssen, E. C. P. Smits, M. Kemerink, D. M. de Leeuw, P. A. Bobbert, Phys. Rev. B. 2010, 82, 075322.

