Odd-Diffusive Systems

Probability distribution and fluxes of a particle diffusing in 2D. The particle starts the origin at t=0. The shaded region in (a) and (b) represents the Gaussian probability distribution at a later time. Arrows show the probability fluxes without magnetic field in (a) and with in (b). Whereas fluxes are typical of a diffusive system in (a), they are curved by the applied magnetic field in (b) which is a hallmark of odd-diffusive systems. The curved flux can be decomposed into a diffusive flux and a rotational flux. The rightmost figure shows the probability density of a pair of interacting particles (hard spheres) diffusing under the effect of Lorentz force at some time t. The initial configuration is shown as white dotted circles. The crosses at the center of the circles show the displacement of the particles. Here collisions between the particles result in a probability flow around each other, somewhat analogous to the swing-by effect. The insets show hidden parts of each particles' curved probability distribution due the overlap in the main figure.

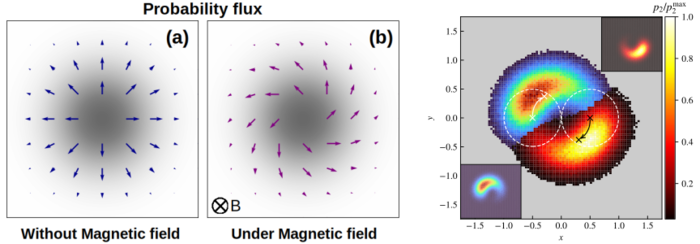
Onsager reciprocal relations imply that diffusion tensors are symmetric. However, the validity of these relations is limited to systems which respect time-reversal symmetry [1]. The motion of a charged particle in a magnetic field is a classical example of the broken time-reversal symmetry. For this reason, the probability flux associated with a particle performing overdamped motion gets a certain handedness based on the charge it carries. Such a diffusion behaviour, also exhibited by active chiral particles, is described by a tensor that has antisymmetric components [2-4]. Analogous to the case of odd-viscosity [5], recently such diffusive behaviour has aptly been termed as odd-diffusive [6] and has attracted considerable attention [7-9].

It is generally believed that collisions of particles reduce the self-diffusion coefficient. We have found that in odd-diffusive systems, collisions can surprisingly enhance the self-diffusion. In these systems, due to an inherent curving effect, the motion of particles is facilitated, instead of hindered by collisions. Consistent with this we also found that the collective diffusion remains unaffected. We are currently working on the effect of odd-diffusivity in polymer chains.

References:

[1] L. Onsager, “Reciprocal relations in irreversible processes. i.,” Physical Review, vol. 37, no. 4, p. 405, 1931.
[2] I. Abdoli, H. D. Vuijk, J. U. Sommer, J. M. Brader, A. Sharma, "Nondiffusive fluxes in a Brownian system with Lorentz force," Phys. Rev. E 101, 012120, 2020.
[3] I. Abdoli, H. D. Vuijk, R. Wittmann, J. U. Sommer, J. M. Brader, A. Sharma, "Stationary state in Brownian systems with Lorentz force," Phys. Rev. Research 2, 2020.
[4] I. Abdoli, A. Sharma, "Stochastic resetting of active Brownian particles with Lorentz force," Soft Matter, 17, 1307-1316, 2021.
[5] J. Avron, “Odd viscosity,” Journal of Statistical Physics, vol. 92, no. 3, pp. 543–557, 1998.
[6] C. Hargus, J. M. Epstein, and K. K. Mandadapu, “Odd diffusivity of chiral random motion,” Phys. Rev. Lett., vol. 127, p. 178001, Oct 2021.
[7] H. Matsuyama and K. Miyazaki, “Anomalous transport phenomenon of a charged Brownian particle under the thermal gradient and the magnetic field,” arXiv preprint arXiv:2109.01807, 2021.
[8] H. D. Vuijk, J.-U. Sommer, H. Merlitz, J. M. Brader, and A. Sharma, “Lorentz forces induce inhomogeneity and flux in active systems,” Physical Review Research, vol. 2, no. 1, p. 013320, 2020.
[9] J.-M. Park and H. Park, “Thermodynamic uncertainty relation in the overdamped limit with a magnetic Lorentz force,” Phys. Rev. Research, p. 043005, 2021.