Biopolymer Networks Mechanics

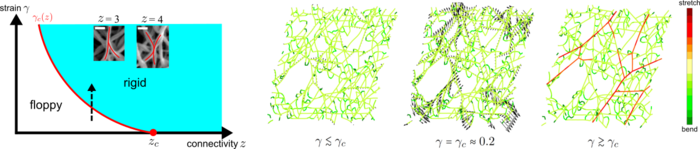
As in a ferromagnetic phase transition, where spontaneous magnetization occurs below the Curie temperature, a disordered fibrous network undergoes a continuous geometric phase transition at a critical strain. The critical strain, which depends on the connectivity z (key structural parameter of athermal networks), defines a line of continuous transitions. Inset shows SEM images of reconstituted collagen networks with 3-fold and 4-fold connectivities. At the transition, indicated by the vertical dashed line, there are divergent non-affine strain fluctuations at the critical strain (right panel).

The elastic response of biological materials is highly nonlinear, exhibiting a strong increase in stiffness with strain. The nonlinear mechanics of the cytoskeletal network inside a cell can be understood on the level of a single fibre [1]. However, despite an abundance of computational studies, there was little insight into the origin of the nonlinear mechanics of extracellular networks and tissues (such as collagen) where thermal fluctuations are relatively insignificant [2].

Recently, we showed that the development of rigidity in sub-isostatic networks is characterised by a strain-controlled continuous phase transition with signatures of criticality [3-5]. Moreover, the nonlinear mechanics of collagen networks can be quantitatively captured by predictions of scaling theory for controlled critical behaviour over a wide range of network concentrations and strains up to failure of the material. In the last 5 years, we have developed a scaling theory for critical behaviour [6], studied the effect of criticality on normal stresses [7] and are currently working on dynamical aspects such as critical slowing down in biopolymer networks.

References:

[1] C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky, and P. A. Janmey, “Nonlinear elasticity in biological gels”, Nature, vol. 435, no. 7039, pp. 191–194, 2005.
[2] C. P. Broedersz and F. C. MacKintosh, “Modeling semiflexible polymer networks,” Reviews of Modern Physics, vol. 86, no. 3, p. 995, 2014.
[3] A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink, F. C. MacKintosh, "Strain-controlled criticality governs the nonlinear mechanics of fibre networks,"Nature Physics, 12, 584, 2016.
[4] A. Sharma, A. J. Licup, R. Rens, M. Vahabi, K. A. Jansen, G. H. Koenderink, and F. C. MacKintosh, "Strain-driven criticality underlies nonlinear mechanics of fibrous networks," Phys. Rev. E 94, 042407, 2016.
[5] K. A. Jansen, A. J. Licup, A. Sharma, R. Rens, F. C. MacKintosh, G. H. Koenderink, "The role of network architecture in collagen mechanics," Biophysical Journal 114, 2665, 2018.
[6] J. Shivers, S. Arzash, A. Sharma, F. C. MacKintosh, "Scaling theory for mechanical critical behavior in fiber networks," Phys. Rev. Lett., 122, 188003, 2019.
[7] J. Shivers, J. Feng, A. Sharma, F. C. MacKintosh, "Normal stress anisotropy and marginal stability in athermal elastic networks," Soft Matter,15, 1666-1675, 2019.