Lorentz force assisted escape of a Brownian particle from a potential well
Methods: Stochastic differential equations, Ito calculus, Kramers escape theory, Stochastic resetting, Brownian Dynamics Simulations
The escape of a Brownian particle over a potential barrier is one of the celebrated problems in nonequilibrium statistical mechanics. In a seminal paper, Kramers showed that escape becomes exponentially rare with increasing barrier height. How does Lorentz force affect the escape dynamics? Lorentz force is a nonconservative, velocity-dependent force which does not perform work on the particle. A well known effect of the Lorentz force is the reduction of the diffusion coefficient in the plane perpendicular to the applied magnetic field [1]. This leads to a trivial rescaling of the escape rate, i.e., it remains exponentially rare with increasing barrier height. Consider that the particle is further subjected to torque. If there is no magnetic field, rotational forces have no effect on the escape dynamics. However, in presence of Lorentz force, the escape dynamics are dramatically modified. Depending on the direction of the magnetic field, the rotating particle may experience an additional nonconservative force towards or away from the origin of the potential due to the Lorentz force. When the force points away from the origin, the escape dynamics become extremely enhanced.
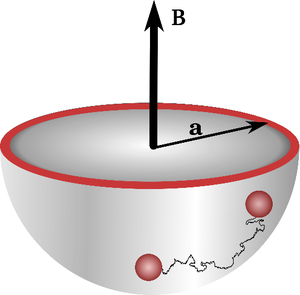
A charged Brownian particle is trapped in a truncated, two dimensional harmonic potential. The particle experiences Lorentz force due to the external magnetic field along z direction. The particle can climb up the potential due to thermal fluctuations and eventually escape on reaching the boundary at r = a. The effect of Lorentz force on the escape process is a further slowing down of the dynamics due to reduction in its diffusion coefficient. Magnetic field, however, does not affect the exponential scaling of the escape rate with the barrier height. Surprisingly, if the particle is further subjected to a nonconservative rotational force, for instance, torque, Lorentz force has a dramatic effect on the escape dynamics: It can enormously enhance the escape rate. Note that without the Lorentz forces, torque alone does not affect the escape dynamics. The goal of the project is to elucidate the mechanism of this surprising effect which has its origin in the coupling between the torque and Lorentz force.
The key tasks of the project are listed below. In principle, these can be divided between two bachelor students.
- Model the escape dynamics in presence of Lorentz force and rotational force. We will use stochastic differential equations for this purpose.
- The effect of Lorentz force can be modeled as a modification of the underlying harmonic potential. Derive the effective potential and perform stability analysis.
- Simulate the escape process using Brownian dynamics.
- Possible extension into a master project via inclusion of an additional stabilising, nonconservative force in form of stochastic resetting [2,3]. Keeping other elements of the problem the same, we include stochastic resetting of the particle back to the origin. In stochastic resetting, a particle is reset to the origin at a given rate. We will perform the first three tasks in this project as well.
Key words: Lorentz force, Magnetic field, Escape, Brownian particle, Torque
References:
[1] I. Abdoli, H. D. Vuijk, J. U. Sommer, J. M. Brader, A. Sharma, "Nondiffusive fluxes in a Brownian system with Lorentz force", Phys. Rev. E 101, 012120, 2020.
[2] I. Abdoli, H. D. Vuijk, R. Wittmann, J. U. Sommer, J. M. Brader, A. Sharma, "Stationary state in Brownian systems with Lorentz force", Phys. Rev. Research 2, 2020.
[3] I. Abdoli, A. Sharma, "Stochastic resetting of active Brownian particles with Lorentz force", Soft Matter, 17, 1307-1316, 2021.

