Methods: Multivariable optimisation, Scaling Theory, Thermodynamic Integration

Disordered random networks are ubiquitous in Biology. These networks major structural components of tissues such as skin and heart and provide mechanical integrity. A very simple model of such networks is a random spring-network as shown in the animation below. The network shown is actually a floppy network. When subjected to small deformations, the network complies; its modulus, i.e., its stiffness is zero. However, beyond a certain deformation (strain), the network becomes rigid. We have recently shown that the transition from floppy to rigid phase is analogous to a continuous phase transition, albeit in an athermal system. One wonders, what happens, when one switches on an auxiliary field, such as the magnetic field in Ising model at the critical point. How does the modulus (order parameter) scale with the auxiliary field in the vicinity of the critical point? We want to find out the effect of (weak) thermal fluctuations on the modulus near the critical point.

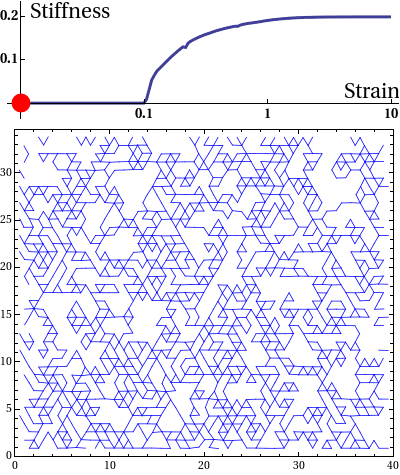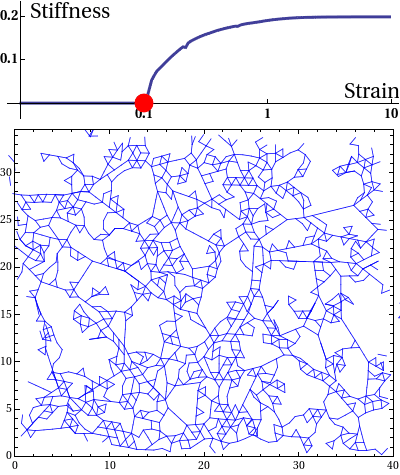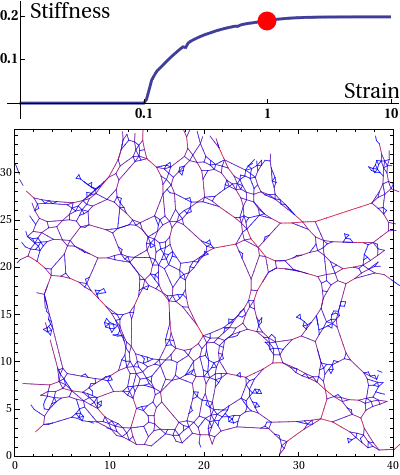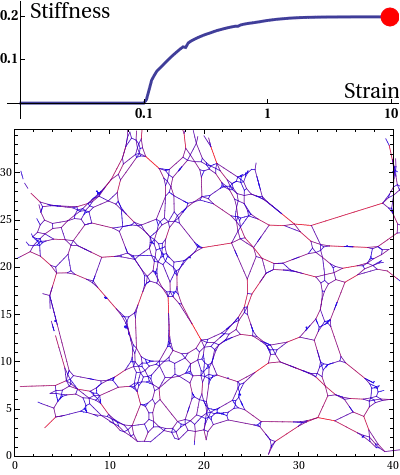
Disordered fibre network subjected to uniform bulk expansion. There is a continuous phase transition from floppy to rigid phase at a critical strain. At the critical strain, the network is infinitely susceptible to external perturbations. How would the network react to thermal fluctuations?

The key tasks of the project are listed below. In principle, the tasks can be divided among two Master students.

1. Simulation of a spring network with a given connectivity subjected to shear deformation.
2. Characterise the stress bearing backbone at the critical strain using tools from the theory of critical phenomena.
3. Include thermal fluctuations and determine how modulus scales with temperature.
4. Scaling analysis of modulus.

Key words: Biopolymer networks, Critical Phenomena, Scaling theory

References:

[1] Sharma, A., Licup, A., Jansen, K. et al., Strain-controlled criticality governs the nonlinear mechanics of fibre networks, Nature Physics, 2016, 12(6), 584-587

[2] Shivers, J. L., Arzash, S., Sharma, A., MacKintosh, F. C., Scaling theory for mechanical critical behaviour in fibre networks, Physical Review Letters, 2019, 122(18), 188003