Methods: Brownian Dynamics Simulations, Fokker-Planck Equation, Stochastic Differential equations, Coarse Graining techniques

Bacteria are evolutionarily advanced organisms. They can sense the direction in which food concentration increases. They accordingly adjust their motion to climb up the food gradients, a phenomenon known as chemotaxis. Active Brownian particles (ABP) are regarded as the simplest model for motility in living organisms. An ABP can be considered as perhaps the minimalistic model of a bacteria. Similar to a bacterium, an ABP performs persistent motion and adjusts its speed according to the local activity (food concentration). However, ABPs don't exhibit chemotaxis. They always accumulate in regions of low activity. We recently found a way to change this behaviour: We simply attached a passive cargo particle to an ABP and found that if the cargo is sufficiently heavy, the dimer (ABP+passive particle) climbs up activity gradients. Our theoretical model considers a permanently attached cargo particle to an ABP. However, a more realistic scenario corresponds to cargo particles attaching and detaching from the ABP. This would result in a distribution of populations: ABPs, Passive particles and Dimers. What we want to find out is how would these three populations be distributed in activity gradients? Imagine: ABPs are all accumulated in low activity regions. A passive cargo attaches to an ABP and the newly formed dimer starts moving up the activity gradients. However, on the way, the cargo detaches leaving the ABP stranded, who wants to migrate back to low activity regions. Interesting dynamics as well as steady state behaviour is expected in such a system.

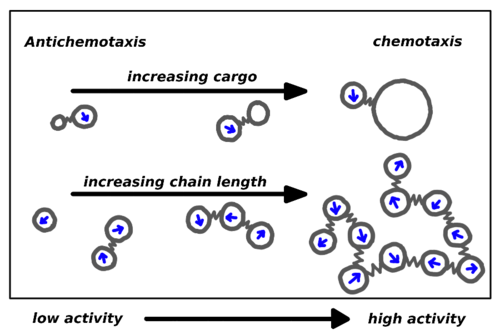
Crossover from antichemotactic to chemotactic behaviour. ABPs are sketched as circles with arrows. Cargo particles (sketched as empty circles) are bound to ABPs. (Above) When the cargo is small, that is, its friction coefficient is small, the dimer accumulates in low activity regions (antichemotaxis). When the cargo is large, the dimer accumulates in the high activity regions (chemotaxis). (Below) Self-emergence of cargo in active chains. When active particles are connected in a chain, one observes the crossover from antichemotactic to chemotactic behaviour with increasing chain length.

The key tasks of the project are listed below. In principle, the tasks can be divided among two Master students.

1. Brownian Dynamics simulations of ABPs + Passive Cargoes in activity gradient. The attachment and detachment kinetics are specified.
2. Brownian Dynamics simulations of ABPs in activity gradient. There are no cargo particles. Two ABPs can attach to each other to form a dumbbell particle. The orientation of the two ABPs becomes frozen after attachment. Subsequently, the dumbbell can disintegrate into two ABPs. For a specified attachment/detachment kinetics, study the dynamics and steady state distribution in activity gradient.
3. Theory Task: For permanently attached passive cargo to an ABP, theoretically determine the work done by the ABP on the cargo, as the dimer moves up the activity gradient. Can the total work be optimised as a function of cargo load? What is the distribution of work?

Key words: Active matter, Brownian Dynamics, Stochastic Thermodynamics, Directed Transport

References:

[1] H. D. Vuijk, H. Merlitz, M. Lang, A. Sharma, and J.-U. Sommer, Chemotaxis of cargo-carrying self-propelled particles, Physical Review Letters, 2021, 126(20), 208102