Mechanical Reinforcement in Filled Polymers
Collaborators
Marina Grenzer (Saphiannikova), Jan Domurath and Vladimir Toshchevikov
Introduction

In most applications of polymer melts and polymer networks rigid filler particles are used to enhance the mechanical properties of the polymer. These filler particles increase the overall mechanical properties of the polymers, e.g. modulus, tensile strength and abrasion resistance. The most prominent example of filled polymers are, probably, tires. The development of such high performance products requires a good understanding of how the filler particles change the properties of the polymer. We are especially interested in the understanding of the hydrodynamic amplification caused by the addition of rigid particles to soft polymer matrices. We use analytical and numerical homogenization methods to determine the effective properties of the filled polymers, by computing the local change of energy and averaging it over the representative volume. The average amplified strain in a polymer matrix can be also computed and compared with analytical predictions. Additionally, we investigate how molecular mobility of polymer networks and thus their dynamical-mechanical properties change upon addition of active fillers. Here we develop a physically based multiscale approach, which allows us to identify structural parameters that show quantitative differences between elastomers reinforced with different fillers.
Cooperations
- Dr. Klaus Werner Stöckelhuber, Department Elastomers
- Prof. Gilles Ausias and Prof. Julien Férec (Université de Bretagne-Sud)
- Dr. Clemens Sill (Goodyear, Luxemburg)
Highlights
- J. Domurath, G. Ausias, J. Férec, M. Saphiannikova
Numerical investigation of dilute suspensions of rigid rods in power-law fluids.
Journal of Non-Newtonian Fluid Mechanics 280 (2020) 104280 - J. Domurath, G. Ausias, J. Férec, G. Heinrich, M. Saphiannikova
A model for the stress tensor in dilute suspensions of rigid spheroids in a generalized Newtonian fluid.
Journal of Non-Newtonian Fluid Mechanics 264 (2019) 73-84 - I. Ivaneiko, V. Toshchevikov, W.K. Stöckelhuber, G. Heinrich, M. Saphiannikova.
Superposition approach to the dynamic-mechanical behaviour of reinforced rubbers.
Polymer 127 (2017) 129-140. - I. Ivaneiko, V. Toshchevikov, S. Westermann, M. Saphiannikova
Multiscale modeling approach to dynamic-mechanical behavior of elastomer nanocomposites.
Springer 275 (2017) 157-186. - J. Domurath, M. Saphiannikova, J. Férec, G. Ausias, G. Heinrich
Stress and strain amplification in a dilute suspension of spherical particles based on a Bird-Carreau model.
Journal of Non-Newtonian Fluid Mechanics 221 (2015) 95-102
Stress and Strain Amplification in Filled Polymers
To describe the non-linear mechanical properties of filled polymer melts we propose a stress and strain amplification approach. In particular, we amplify both the stress and strain in the constitutive relation for the unfilled polymer melt to account for the presence of rigid filler particles. We use numerical simulations to validate our approach and to propose new methods of modification of the constitutive equations.
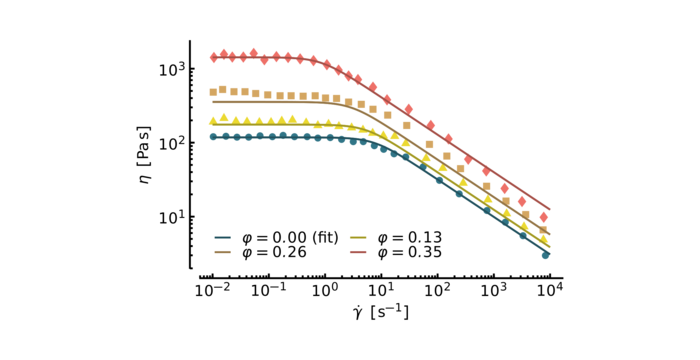
Spherical particles
The figure below shows the comparison of our proposed modification of the Carreau model with experimental results of Poslinsky et al. \[ \eta = X(\varphi)\,\eta_0 \left(1 + [a_\text{d}(\varphi, n)\,\lambda \dot{\gamma}]^{2}\right)^{n/2} \]
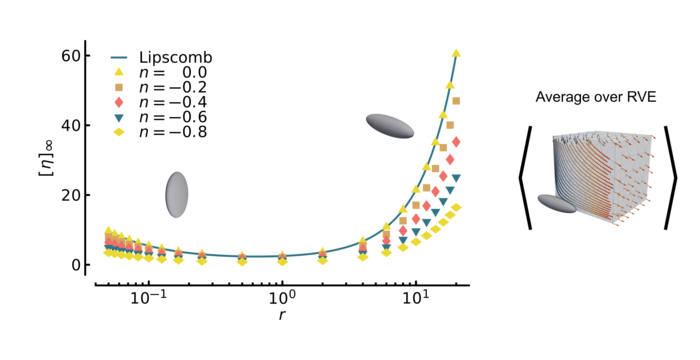
Spheroidal particles
We also investigate non-spherical particles in gerneralized Newtonian fluids. The figure shows the values of the intrinsic viscosity for spheroids of different aspect ratios \(r\) in a power-law fluid.
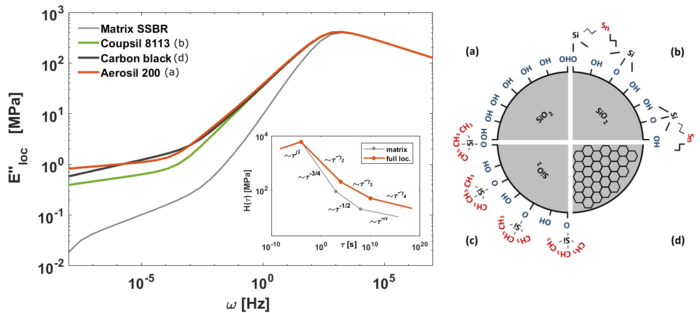
Multiscale Approach to Dynamics of Reinforced Elastomers
The investigation of the molecular mobility of polymer chains and networks in the presence of active fillers such as carbon black or silica presents a big interest for the physics of reinforced elastomers. A better understanding of the physical characteristics of the filler-rubber interface is necessary to improve the overall macroscopic properties of these elastomers. We aim to develop a physically based multiscale approach for description of the enhanced viscoelastic properties of reinforced elastomers. This approach takes into account contributions from the glassy, bending, localized Rouse-like and long-time relaxation regimes. For unfilled rubbers we interpret the latter regime in the frame of entangled dangling chain concept found to be valid for randomly cross-linked rubbers. For filled rubbers the exponent decreases due to appearance of filler aggregates. The proposed multi-scale approach allows to extract from experimental data a set of fundamental structural characteristics of polymer network and their change upon addition of filler.